|
Hierarchische Strukturen werden oft in Form von Baumgrafen (treemaps) dargestellt. Ein typisches Beispiel für eine hierarchische Struktur ist das Dateisystem einer Festplatte mit Hauptverzeichnis, Unterverzeichnissen und Dateien. Oft wird diese Struktur in Datei-Browsern als Baum dargestellt, wie z.B. auch im Explorer von Microsoft, der der Standard-Datei-Browser des Betriebssystems Windows ist.
Um sich einen Überblick über eine gesamte Festplatte zu verschaffen - zum Beispiel um die Frage zu beantworten, warum sie schon wieder so voll ist - bedarf es schon in normalen Fällen vieler Manöver, um alle Unterverzeichnisse auf ihren Inhalt hin durchzusehen. Ein Anzeigen aller Dateien absteigend der Größe nach sortiert muss nicht zum Ziel führen, wenn der überwiegende Teil des Festplattenplatzes durch kleine Dateien, die aber sehr zahlreich sind und sich ggf. nur in wenigen Unterordner befinden, repräsentiert wird. Die Darstellung einer hierarchischen Struktur durch gewöhnliche Baumdiagramme verschafft einen also nur in glücklichen Fällen einen schnellen Überblick. Die Zahl der Fälle, in denen ein schneller Überblick gelingt, kann durch Verwendung spezieller treemaps, sogenannter squarified treemaps stark vergrößert werden [11].

|
Treemaps setzen die hierarchische Struktur statt in eine Baumstruktur in eine Karte um. Dabei werden die hierarchischen Ebenen durch Rechtecke repräsentiert, die durch ihre Schachtelung die hierarchische Struktur wiederspiegeln. Die Fläche der Rechtecke kann dabei, um beim Beispiel des Dateisystems zu bleiben, die Größe oder Anzahl der Dateien darstellen. Wichtig ist, das diese Größe über die Hierarchieebenen additiv ist, d.h. diese Größe muss für ein Element in einer bestimmten Hierarchieebene die Summe aller Elemente aus der nächsten tiefer liegenden Hierarchieebene sein. Damit ist z.B. die Darstellung der durchschnittlichen Dateigröße durch treemaps nicht darstellbar.
Bei squarified treemaps wird versucht die Form der Rechtecke möglichst wenig von Quadraten abweichen zu lassen, da dies sich günstig auf die visuelle Erscheinung der treemap auswirkt (siehe Abbildung 2.7 unten). Diese Optimierung wird durch einen Algorithmus durchgeführt, der zwar keine optimale Lösung garantiert, aber im Normalfall unter vertretbarem Aufwand brauchbare Ergebnisse liefert ([11] ab Seite 33).
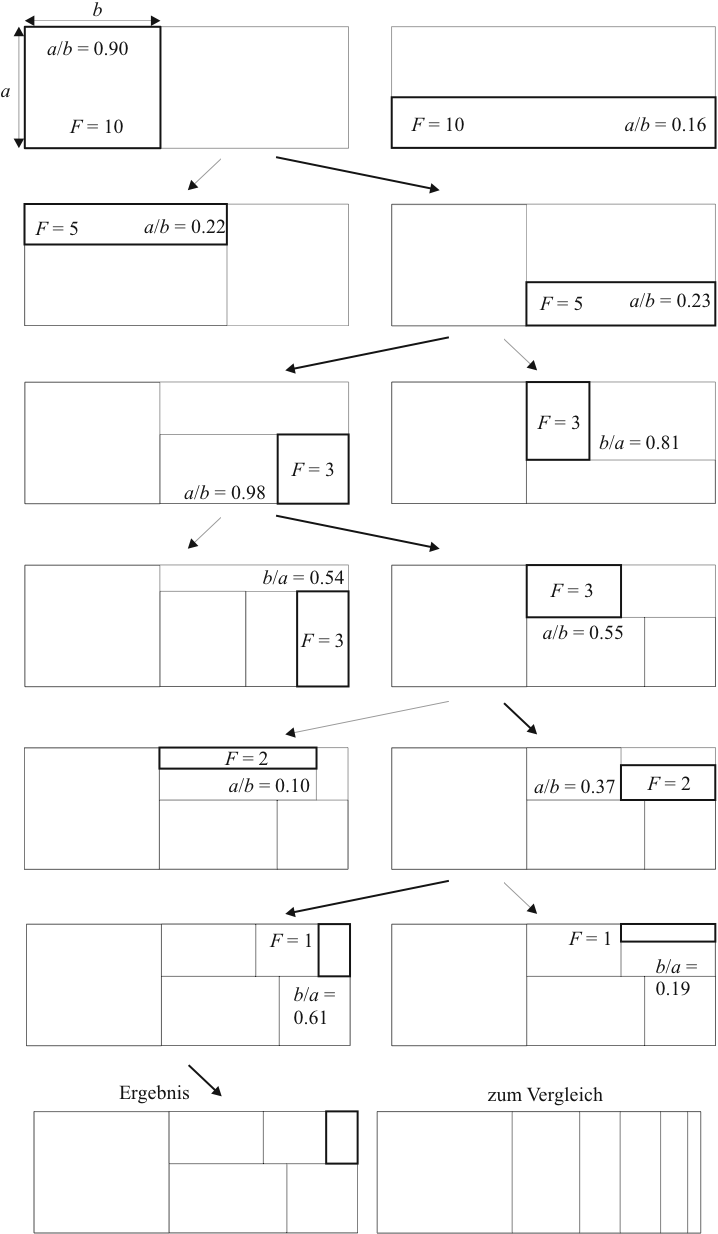
Abbildung 2.7 zeigt an einem Beispiel, wie der Algorithmus arbeitet. In diesem Beispiel werden nur die Rechtecke einer Hierarchieebene in ein großes Rechteck eingepasst. Das Beispiel lässt sich aber leicht auf eine hierarchische Struktur mit mehreren Ebenen erweitern, indem man das Vorgehen des Beispiels iterativ auf die erzeugten Teilrechtecke anwendet und so eine Darstellung einer hierarchischen Struktur erzeugt.
In diesem Beispiel soll eine Hierarchieebene mit 6 Elementen
Dargestellt werden, denen die Größen 10, 5, 3, 3, 2 und 1
zugeordnet sind. Die Rechtecke sollen in ein Rechteck mit
Seitenverhältnis 8/3 eingepasst werden. Die Fläche aller
Teilrechtecke ergibt die Fläche des Gesamtrechtecks. Beispielhaft
sind an diesem Rechteck auch noch die Seitenlängen ![]() und
und ![]() eingezeichnet, aus denen das später benötigte Seitenverhältnis
bestimmt werden kann. Dazu werden die Elemente der Größe nach
absteigend in das Rechteck eingepasst. In der ersten Zeile der
Abbildung 2.7 wird das größte Teilrechteck mit
der Fläche 10 entsprechend seiner Größe in das Gesamtrechteck
eingezeichnet. Es gibt zwei Möglichkeiten, dies zu tun. Hier wird
die Möglichkeit mit dem ausgewogensten Verhältnis von
eingezeichnet, aus denen das später benötigte Seitenverhältnis
bestimmt werden kann. Dazu werden die Elemente der Größe nach
absteigend in das Rechteck eingepasst. In der ersten Zeile der
Abbildung 2.7 wird das größte Teilrechteck mit
der Fläche 10 entsprechend seiner Größe in das Gesamtrechteck
eingezeichnet. Es gibt zwei Möglichkeiten, dies zu tun. Hier wird
die Möglichkeit mit dem ausgewogensten Verhältnis von ![]() und
und ![]() gewählt.
gewählt.
Nun wird das nächste kleinere Rechteck eingepasst. In Zeile zwei
der Abbildung 2.7 sind dafür zwei Möglichkeiten
angegeben: einmal kann das nächste Rechteck über dem Vorherigen
eingepasst werden - beide Rechtecke haben dann die gleiche
horizontale Kantenlänge, oder es kann daneben eingepasst werden.
Für beide Alternativen ergeben sich unterschiedliche
Seitenverhältnisse ![]() . Für den Fall, dass
. Für den Fall, dass ![]() ist wird
im folgenden einfach der Kehrwert
ist wird
im folgenden einfach der Kehrwert ![]() betrachtet. Die
Seitenverhältnisse sind also immer kleiner oder gleich eins. Um zu
entscheiden, welche Alternative gewählt wird, um das neue Rechteck
anzufügen, wird das Seitenverhältnis herangezogen, da es
ermöglicht optisch leichter zu erfassende Rechtecke mit
ausgeglichenem Seitenverhältnis nahe bei 1 gegenüber länglicheren
zu bevorzugen. In diesem Auswahlschritt findet die
,,squarification`` statt - die Rechtecke sollen so eingepasst
werden, dass sie möglichst eine quadratische Form erhalten.
betrachtet. Die
Seitenverhältnisse sind also immer kleiner oder gleich eins. Um zu
entscheiden, welche Alternative gewählt wird, um das neue Rechteck
anzufügen, wird das Seitenverhältnis herangezogen, da es
ermöglicht optisch leichter zu erfassende Rechtecke mit
ausgeglichenem Seitenverhältnis nahe bei 1 gegenüber länglicheren
zu bevorzugen. In diesem Auswahlschritt findet die
,,squarification`` statt - die Rechtecke sollen so eingepasst
werden, dass sie möglichst eine quadratische Form erhalten.
Dieser Schritt wird für die folgenden und kleiner werdenden Rechtecke wiederholt, wie in den folgenden Zeilen der Abbildung 2.7 dargestellt. Rechtecke können dabei sowohl horizontal als auch vertikal angefügt werden.
In der letzten Zeile ist das Endergebnis dargestellt und zum Vergleich das Ergebnis, das man erhält, wenn man die Flächenaufteilung wie in einem gewöhnlichen Balkendiagramm vornimmt. Insbesondere bei den sehr schmalen Teilrechtecken ist das Einpassen einer weiteren tieferen Hierarchieebene in optische ansprechender Form kaum noch möglich.
|
|
Soll die Anzahl der Geräte nach kategorialen Merkmalen wie z.B. ,,Krankenhaus`` und ,,Gerätebezeichnung`` gruppiert angegeben werden, so eignen sich zur Darstellung dieser Zahlen Balkendiagramme. Ein Balken repräsentiert dann z.B. ein Krankenhaus, und die Rechtecke, aus denen ein Balken zusammengesetzt ist, repräsentieren die Anzahl der Geräte in den betrachteten Gerätegruppen des Krankenhauses. Möchte man nicht die absoluten sondern die relativen Geräteanzahlen vergleichen, so normiert man die Gesamtzahl der Geräte in einem Krankenhaus auf 100%. Die tabellarische Anordnung dieser Zahlen nennt man Kreuz- oder Pivot-Tabelle.
Ein Problem bei der Darstellung einer Kreuztabelle durch ein
Balkendiagramm ist, dass es sehr viele verschiedene Möglichkeiten
gibt die Kreuztabelle darzustellen. Da die Kategorien keine
natürliche Ordnung besitzen, können sie beliebig angeordnet
werden. Für eine Kreuztabelle mit dem Merkmal A (![]() verschiedene Kategorien) und Merkmal B (
verschiedene Kategorien) und Merkmal B (![]() verschiedene
Kategorien) ergibt sich eine Anzahl von
verschiedene
Kategorien) ergibt sich eine Anzahl von ![]() verschiedenen
Anordnungen der Kategorien mit jeweils verschiedenen
Balkendiagrammen. Welches Diagramm ist für eine übersichtliche
Darstellung der Zahlen zu wählen?
verschiedenen
Anordnungen der Kategorien mit jeweils verschiedenen
Balkendiagrammen. Welches Diagramm ist für eine übersichtliche
Darstellung der Zahlen zu wählen?
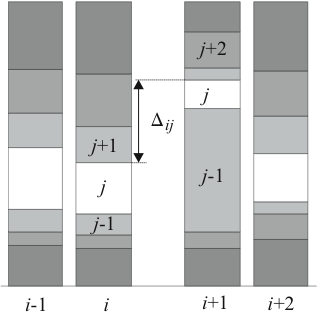
Günstig auf die visuelle Wahrnehmung wirkt es sich aus, wenn das Balkendiagramm einen möglichst geordneten Eindruck macht - insbesondere lassen sich so auch leicht Gruppen von Kategorien erkennen. Der Eindruck eines geordneten Balkendiagramms lässt sich zumindest näherungsweise dadurch erreichen, dass man die Sortierung der Kategorien so wählt, dass die Rechteckkanten zu gleichen Kategorien benachbarter Spalten möglichst dicht beieinander liegen (siehe Abbildung 2.8). Diese Minimalbedingung lässt sich mit den Bezeichnungen aus Abbildung 2.8 schreiben als
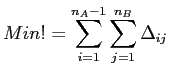 |
(43) |
Die Spalten sind dabei von ![]() bis
bis ![]() und die
Rechtecke der Spalten mit
und die
Rechtecke der Spalten mit ![]() bis
bis ![]() numeriert. Für auf
100% normierte Balken sind die
numeriert. Für auf
100% normierte Balken sind die
![]() , da die Spalten
alle gleich hoch sind.
, da die Spalten
alle gleich hoch sind.
Diese Summe ist nun für alle Permutationen
der Kategorien der Merkmale ![]() und
und ![]() zu bestimmen. Für
zu bestimmen. Für
![]() ergeben sich ca. 0.5 Millionen Möglichkeiten. Für
ergeben sich ca. 0.5 Millionen Möglichkeiten. Für
![]() sind es schon ca. 25 Millionen und für
sind es schon ca. 25 Millionen und für ![]() sind es gar 16 000 Millionen. Will man mittels ,,brute-force``
das Minimum ermitteln, so ist das nur noch bei sieben Kategorien
pro Merkmal mit zeitlich vertretbarem aufwand möglich. Sollen
Merkmale untersucht werden, die über mehr als sieben Kategorien
verfügen, so können bis auf die sechs häufigsten Kategorien alle
restlichen in der siebten Kategorie ,,sonstige`` zusammengefasst
werden (siehe Abbildung 2.9).
sind es gar 16 000 Millionen. Will man mittels ,,brute-force``
das Minimum ermitteln, so ist das nur noch bei sieben Kategorien
pro Merkmal mit zeitlich vertretbarem aufwand möglich. Sollen
Merkmale untersucht werden, die über mehr als sieben Kategorien
verfügen, so können bis auf die sechs häufigsten Kategorien alle
restlichen in der siebten Kategorie ,,sonstige`` zusammengefasst
werden (siehe Abbildung 2.9).
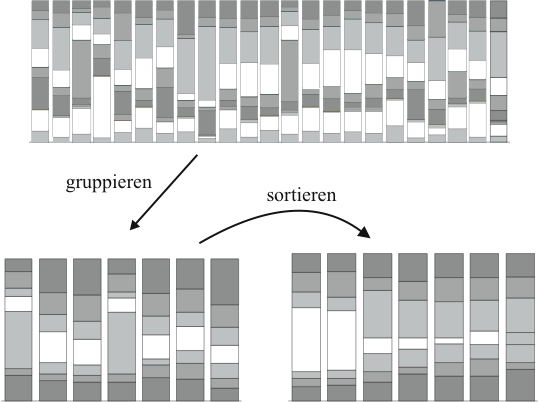
Einen Algorithmus, der auch für größere Anzahlen von Kategorien eine wenn auch nicht optimale aber dennoch brauchbare Lösung bei vertretbarer Laufzeit ermittelt, konnte in dieser Arbeit nicht gefunden werden. Das Problem hat Ähnlichkeit zum Traveling-Salesman-Problem, für das eine Reihe solcher Lösungen existiert. Da bei diesem Problem jedoch nicht nur ein Merkmal sondern zwei zu sortieren sind, können die Algorithmen zur Lösung von Traveling-Salesman-Problemen nicht verwendet werden. Das entwickeln eines neuen Algorithmus ist im Rahmen dieser Arbeit nicht gelungen. Es zeigt sich aber auch häufig, dass ab der sechst-häufigsten Kategorie die Häufigkeiten schon so stark abgefallen sind, das das Diagramm davon kaum noch beeinflusst wird.
Hat man Entitäten oder Gruppen von Entitäten ![]() , denen zwei
metrische Merkmale
, denen zwei
metrische Merkmale ![]() und
und ![]() zugeordnet werden können, so
ist zunächst die Frage von Interesse, ob zwischen diesen
Merkmalen ein Zusammenhang (Korrelation) besteht. In diesen Fällen
hilft die Korrelations- oder Regressionsanalyse weiter. Zum
Beispiel können die
zugeordnet werden können, so
ist zunächst die Frage von Interesse, ob zwischen diesen
Merkmalen ein Zusammenhang (Korrelation) besteht. In diesen Fällen
hilft die Korrelations- oder Regressionsanalyse weiter. Zum
Beispiel können die ![]() Gerätegruppen sein, Merkmal
Gerätegruppen sein, Merkmal ![]() kann
die Anzahl der Geräte und Merkmal
kann
die Anzahl der Geräte und Merkmal ![]() kann die Summe der
Kaufpreise der Geräte sein jeweils für die Gruppe
kann die Summe der
Kaufpreise der Geräte sein jeweils für die Gruppe ![]() . Findet
sich nun ein linearer Zusammenhang zwischen
. Findet
sich nun ein linearer Zusammenhang zwischen ![]() und
und ![]() , so
kann man die Steigung dieses linearen Zusammenhangs als über die
Gerätegruppen hinweg existenten mittleren Kaufpreises pro Gerät
interpretieren, den man durch eine Regressionsanalyse bestimmen
kann.
, so
kann man die Steigung dieses linearen Zusammenhangs als über die
Gerätegruppen hinweg existenten mittleren Kaufpreises pro Gerät
interpretieren, den man durch eine Regressionsanalyse bestimmen
kann.
Lässt sich jedoch keine Korrelation zwischen den Merkmalen
finden, so kann man dennoch ggf. wertvolle Informationen
gewinnen: Es liegt eine ausreichend deutliche Ungleichverteilung
der Merkmale ![]() und
und ![]() in den Gruppen
in den Gruppen ![]() vor, die eine
Einteilung in verschiedene neue Gruppen erlaubt. Es können im
obigen Beispiel sich für die verschiedenen Gerätegruppen deutlich
unterschiedliche mittlere Kaufpreise ergeben, die Anzahl der
Geräte also unabhängig von der Summe der Kaufpreise sein.
Gegebenenfalls sind die Unterschiede der mittleren Kaufpreise
sogar so groß, dass sie eine neue Einteilung der Gerätegruppen
rechtfertigen.
vor, die eine
Einteilung in verschiedene neue Gruppen erlaubt. Es können im
obigen Beispiel sich für die verschiedenen Gerätegruppen deutlich
unterschiedliche mittlere Kaufpreise ergeben, die Anzahl der
Geräte also unabhängig von der Summe der Kaufpreise sein.
Gegebenenfalls sind die Unterschiede der mittleren Kaufpreise
sogar so groß, dass sie eine neue Einteilung der Gerätegruppen
rechtfertigen.
Zur Beurteilung der Stärke der Ungleichverteilung sollen die im folgenden vorgestellten Lorenzkurve und der Gini-Koeffizient verwendet werden (z.B. [12] Seite 52).
|
Zum Erstellen einer Lorenzkurve sortiert man die Gruppen ![]() mit
mit
![]() aufsteigend oder absteigend nach dem
Quotienten
aufsteigend oder absteigend nach dem
Quotienten ![]() . Dann ordnet man den sortierten
. Dann ordnet man den sortierten ![]() jeweils
die kumulierten
jeweils
die kumulierten
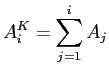 und und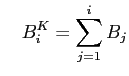 |
(44) |
zu. Dann kann man die kumulierten ![]() und
und ![]() noch als
noch als
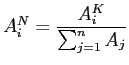 und und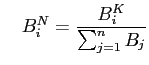 |
(45) |
auf eins normieren und als sog. ,,Lorenz- oder
Konzentrationskurve`` mit Definitions- und Wertebereich
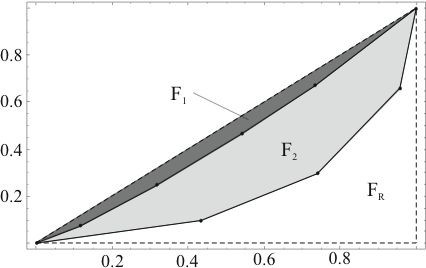
![]() auftragen. Als Beispiel sind in Abbildung
2.10 zwei Lorenzkurven zu den Werten ((5,45),
(7,91), (3,20), (6,62), (5,57) und zu den Werten ((10,21),
(1,71), (5,77), (7,12)) angegeben. Die größere Ungleichverteilung
in der zweiten Wertereihe lässt sich anhand der stärker gebogenen
Lorenzkurve deutlich erkennen. Zur objektiven Beurteilung der
Wölbung kann man die in Abbildung 2.10
eingezeichneten Flächen heranziehen: je größer die
Ungleichverteilung desto größer die Wölbung der Lorenzkurve desto
größer die Fläche zwischen Lorenzkurve und der gedachten Line
durch die Punkte (0,0) und (1,1). Diese Fläche wird als
,,lorenzisches Konzentrationsmaß`` oder ,,Gini-Koeffizient``
bezeichnet.
auftragen. Als Beispiel sind in Abbildung
2.10 zwei Lorenzkurven zu den Werten ((5,45),
(7,91), (3,20), (6,62), (5,57) und zu den Werten ((10,21),
(1,71), (5,77), (7,12)) angegeben. Die größere Ungleichverteilung
in der zweiten Wertereihe lässt sich anhand der stärker gebogenen
Lorenzkurve deutlich erkennen. Zur objektiven Beurteilung der
Wölbung kann man die in Abbildung 2.10
eingezeichneten Flächen heranziehen: je größer die
Ungleichverteilung desto größer die Wölbung der Lorenzkurve desto
größer die Fläche zwischen Lorenzkurve und der gedachten Line
durch die Punkte (0,0) und (1,1). Diese Fläche wird als
,,lorenzisches Konzentrationsmaß`` oder ,,Gini-Koeffizient``
bezeichnet.
Neben dem Gini-Koeffizienten gibt es noch eine Reihe anderer
Ungleichverteilungskoeffizienten. Ein Vorteil des
Gini-Koeffizienten - seine anschauliche Interpretation als
Fläche der Lorenzkurve kann auch als Nachteil gedeutet werden:
der Zahlenwert hat keine praktische Bedeutung und besitzt eine
komplizierte Berechnungsvorschrift. Diese Nachteile besitzt der
Hoover-Ungleichverteilungskoeffizient ![]() nicht [13]. Er
berechnet sich zu
nicht [13]. Er
berechnet sich zu
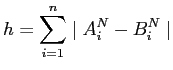 |
(46) |
Die Berechnung des Koeffizienten ist einfach und damit transparenter als beim Gini-Koeffizienten. Außerdem kann man den Zahlenwert des Hoover-Koeffizienten als den Anteil interpretieren, der umverteilt werden muss, um eine Gleichverteilung zu erhalten.
Andere Koeffizienten quantifizieren die Ungleichverteilung anhand von Entropiebetrachtungen der zu untersuchenden Verteilung. Diese Koeffizienten lassen rich zwar schlüssig aus der Theorie ableiten, setzten aber auf den wenig anschaulichen Begriff der Entropie auf und werden deswegen in dieser Arbeit nicht zur Untersuchung herangezogen.