|
Die DIN 31051 unterteilt die Aufgaben der Instandhaltung in drei Bereiche [7] (Seite 22ff):

|
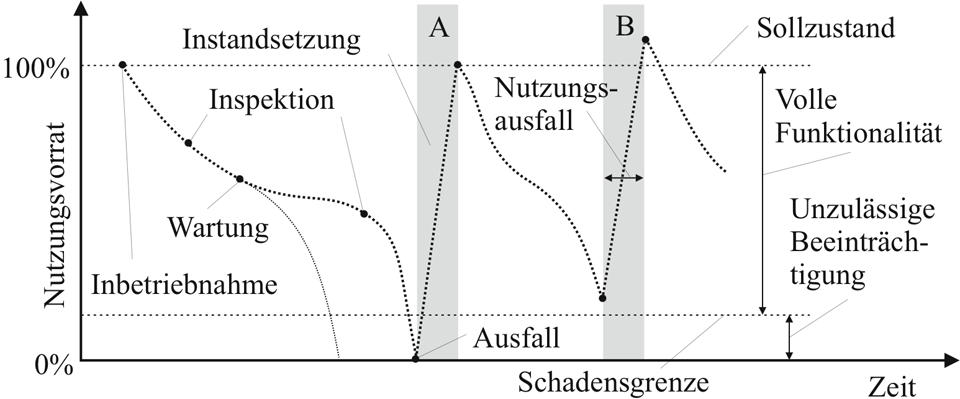
In der Abbildung 2.4 sind die oben genannten Begriffe an einem Ausschnitt eines Gerätelebenslaufes dargestellt. Bei der Inbetriebnahme eines neuen Gerätes beträgt der Nutzungsvorrat 100% - das Gerät befindet sich im Sollzustand. Während der Nutzung des Gerätes sinkt der Nutzungsvorrat. Dieser kann durch Inspektionen ermittelt werden. Durch Wartungen kann die Abnahme des Nutzungsvorrates vermindert werden. Ein idealisierter Verlauf des Nutzungsvorrates ohne Wartung ist durch die dünne Linie angedeutet. Unterschreitet der Nutzungsvorrat die Schadensgrenze, so ist eine volle Funktionalität des Gerätes nicht mehr gewährleistet - ab jetzt muss mit unzulässigen Beeinträchtigungen gerechnet werden, bis schließlich der Ausfall des Gerätes eintritt. Durch eine Instandsetzung kann ein ausgefallenes Gerät wieder in den Sollzustand versetzt werden (A). Durch geeignete Maßnahmen kann der Nutzungsvorrat auch auf über 100% erhöht werden (B). Instandsetzungen können selbstverständlich auch vor Ausfall eines Gerätes erfolgen. Der zeitliche Verlauf des Nutzungsvorrates muß nicht, wie in der Darstellung angegeben, stetig verlaufen.
Bei der EDV gestützten Instandhaltung fallen viele Informationen an. Um diese Informationen für nötige Entscheidungen in Hinblick auf eine wirtschaftliche Bewirtschaftung nutzbar zu machen, müssen die oft verstreuten Informationen in brauchbarer Form zusammengefasst werden. Dies sollen Kenngrößen leisten. Die wichtigsten, etablierten Kenngrößen lauten [8]:
|
Zum Zeitpunkt ![]() mögen sich
mögen sich ![]() Geräte in Betrieb befinden. Zu
diskreten Zeitpunkten
Geräte in Betrieb befinden. Zu
diskreten Zeitpunkten ![]() wird festgestellt, wie viele
Geräte seit der letzten Untersuchung zum Zeitpunkt
wird festgestellt, wie viele
Geräte seit der letzten Untersuchung zum Zeitpunkt
![]() ausgefallen sind. Die Zahl nennen wir
ausgefallen sind. Die Zahl nennen wir ![]() . Dann können wir den
Anteil
. Dann können wir den
Anteil ![]() der bis jetzt ausgefallenen und den Anteil der noch
laufenden Geräte
der bis jetzt ausgefallenen und den Anteil der noch
laufenden Geräte ![]() an allen
an allen ![]() Geräten bestimmen. Dabei gilt:
Geräten bestimmen. Dabei gilt:
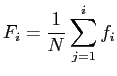 und und |
(30) |
nun kann die Ausfallrate ![]() bestimmt werden:
bestimmt werden:
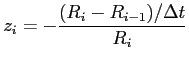 |
(31) |
Für den Divisor ![]() wäre
wäre
![]() zwar korrekter,
da auch die numerische Ableitung in der Mitte des Zeitintervalls
zwar korrekter,
da auch die numerische Ableitung in der Mitte des Zeitintervalls
![]() bestimmt wird, aber für kleine
bestimmt wird, aber für kleine
![]() ist der dadurch zu erwartende Fehler vertretbar. Die
Ausfallrate gibt die Wahrscheinlichkeit an, mit der ein Gerät bis
zur nächsten Untersuchung ausgefallen ist. Dies ist eine wichtige
Information für die Gerätebewirtschaftung. Durch die Funktion
([7] Seite 129)
ist der dadurch zu erwartende Fehler vertretbar. Die
Ausfallrate gibt die Wahrscheinlichkeit an, mit der ein Gerät bis
zur nächsten Untersuchung ausgefallen ist. Dies ist eine wichtige
Information für die Gerätebewirtschaftung. Durch die Funktion
([7] Seite 129)
| (32) |
erhalten wir eine stetige Verteilungsfunktion der
reellwertigen Zufallsvariablen ![]() . Hierbei ist
. Hierbei ist
![]() die
Wahrscheinlichkeit, dass der Ausfallzeitpunkt
die
Wahrscheinlichkeit, dass der Ausfallzeitpunkt ![]() vor dem
Betrachtungszeitpunkt
vor dem
Betrachtungszeitpunkt ![]() liegt. Damit ergibt sich
liegt. Damit ergibt sich
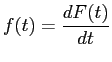 |
(33) |
und analog zu den oben eingeführten diskreten Größen kann man schreiben:
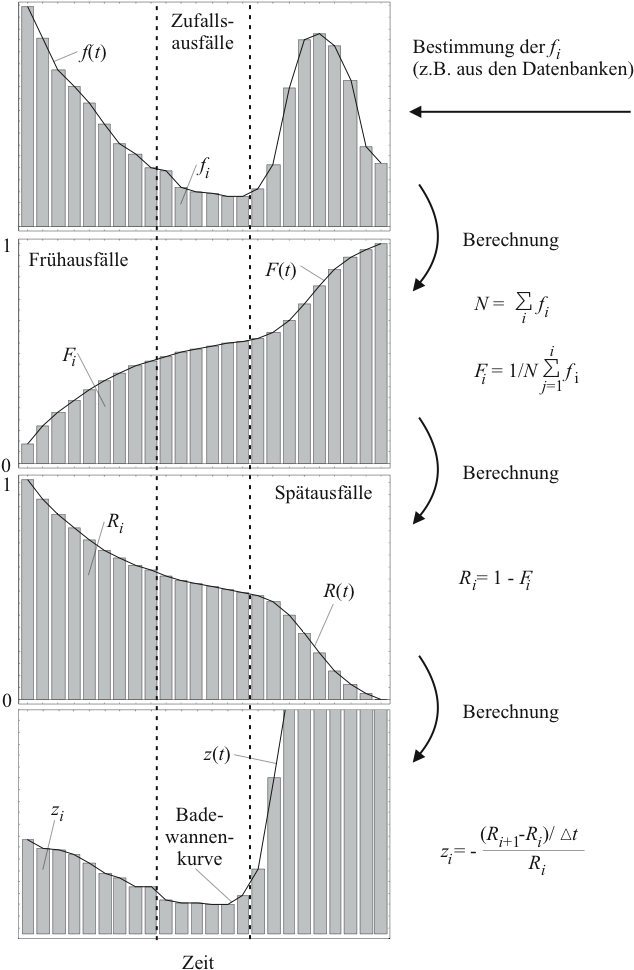
Die vorgestellten diskreten und stetigen Zusammenhänge sind zur
Veranschaulichung in Abbildung 2.5 dargestellt. In
der obersten Grafik ist die diskrete Anzahl ![]() bzw.
kontinuierliche Anzahl
bzw.
kontinuierliche Anzahl ![]() der ausgefallen Geräte pro Zeit
aufgetragen. In der zweiten Grafik von oben ist die kumulierte
Anteil
der ausgefallen Geräte pro Zeit
aufgetragen. In der zweiten Grafik von oben ist die kumulierte
Anteil ![]() bzw.
bzw. ![]() der ausgefallenen Geräte angegeben. Die
oberste Verlauf ergibt sich somit als Ableitung des zweiten
Verlaufes von oben. Die dritte Grafik gibt die Anzahl
der ausgefallenen Geräte angegeben. Die
oberste Verlauf ergibt sich somit als Ableitung des zweiten
Verlaufes von oben. Die dritte Grafik gibt die Anzahl ![]() bzw.
bzw.
![]() der Geräte ohne Ausfall an. Aus diesem Zusammenhang lässt
sich leicht die in der unteren Grafik angegebene Ausfallrate
der Geräte ohne Ausfall an. Aus diesem Zusammenhang lässt
sich leicht die in der unteren Grafik angegebene Ausfallrate
![]() bzw.
bzw. ![]() ermitteln. Die zahlen in diesem Beispiel sind
so gewählt, dass sich in der untersten Grafik die sogenannte
Badewannenkurve ergibt. Nach einer ,,Einbrennphase``
fällt in der
,,Nutzungsphase`` die
Ausfallrate zunächst ab, um dann in der ,,Verschleissphase``
wieder anzusteigen.
ermitteln. Die zahlen in diesem Beispiel sind
so gewählt, dass sich in der untersten Grafik die sogenannte
Badewannenkurve ergibt. Nach einer ,,Einbrennphase``
fällt in der
,,Nutzungsphase`` die
Ausfallrate zunächst ab, um dann in der ,,Verschleissphase``
wieder anzusteigen.
In [7] (Seite 130) wird der Verlauf der Ausfallrate
![]() in drei Bereiche eingeteilt:
in drei Bereiche eingeteilt:
Dabei ist zu beachten, dass die Zeit ![]() bei den
bisherigen Betrachtungen immer seit dem letzten Ausfall gemessen
wurde. Nach einem Ausfall und darauf folgender Instandsetzung
wird die Zeit wieder von Null an gemessen. Es wird so getan, als
ob das Gerät nach einer Instandsetzung wieder neu (
bei den
bisherigen Betrachtungen immer seit dem letzten Ausfall gemessen
wurde. Nach einem Ausfall und darauf folgender Instandsetzung
wird die Zeit wieder von Null an gemessen. Es wird so getan, als
ob das Gerät nach einer Instandsetzung wieder neu (![]() ) ist -
also kein Gedächtnis besitzt. Diese Annahme muss durchaus kritisch
beurteilt werden.
) ist -
also kein Gedächtnis besitzt. Diese Annahme muss durchaus kritisch
beurteilt werden.
Möchte man die Ausfallrate nicht in Abhängigkeit der Zeit seit dem letzten Ausfall untersuchen sondern seit Inbetriebnahme des betroffenen Gerätes, so kann man eine Ersatzausfallrate
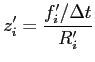 |
(36) |
bestimmen, bei der die ![]() die Anzahl der Ausfälle im Zeitraum
die Anzahl der Ausfälle im Zeitraum
![]() nach Inbetriebnahme des betroffenen
Gerätes und
nach Inbetriebnahme des betroffenen
Gerätes und ![]() die Anzahl der noch laufenden Geräte zum
Zeitpunkt
die Anzahl der noch laufenden Geräte zum
Zeitpunkt
![]() nach ihrer Inbetriebnahme ist.
nach ihrer Inbetriebnahme ist. ![]() gibt
dann die Anzahl der Ausfälle pro Gerät und Zeitraum in
Abhängigkeit der Betriebszeit an - und nicht in Abhängigkeit der
Zeit seit der letzten Maßnahme.
gibt
dann die Anzahl der Ausfälle pro Gerät und Zeitraum in
Abhängigkeit der Betriebszeit an - und nicht in Abhängigkeit der
Zeit seit der letzten Maßnahme.
Die Mean Time Between Failures(MTBF) bezeichnet den Mittelwert der Lebensdauer. Für stetige Zufallsvariablen kann man die MTBF folgendermaßen ermitteln
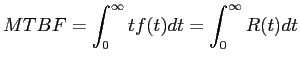 |
(37) |
Für diskrete Zufallsvariablen ergibt sich
Der dabei begangene Fehler durch Lage der
Betrachtungszeitpunkte der ![]() und
und ![]() am Anfang der
Zeitintervalle
am Anfang der
Zeitintervalle
![]() statt in der Mitte
ist für kleine
statt in der Mitte
ist für kleine ![]() vernachlässigbar.
vernachlässigbar.
|
Betrachten wir den einfachen Fall konstanter Ausfallquote
![]() . Dann ergibt sich aus Formel 2.35
. Dann ergibt sich aus Formel 2.35
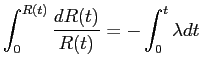 |
(39) |
und durch Integration
| (40) |
Für Konstante Ausfallraten
![]() ergibt sich
also die Überlebenswahrscheinlichkeit
ergibt sich
also die Überlebenswahrscheinlichkeit
![]() als
Exponentialverteilung. Für die MTBF ergibt sich
als
Exponentialverteilung. Für die MTBF ergibt sich
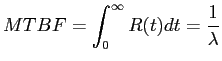 |
(41) |
Neben der Exponentialverteilung gibt es noch eine Reihe anderer Verteilungen. Einen bewährten Kompromiss zwischen einfacher Darstellung und Anpassungsfähigkeit stellt die Weibull-Verteilung dar:
| (42) |
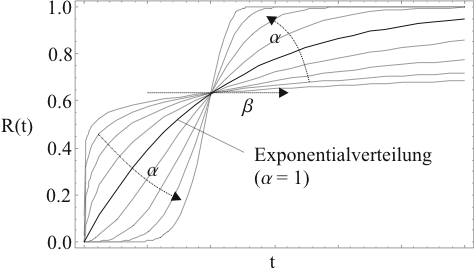
Die Wirkung der beiden Parameter ist in Abbildung
2.6 dargestellt. Durch ![]() kann man
festlegen ob die Ausfallquote mit der Zeit ansteigt (überwiegend
Verschleissausfälle,
kann man
festlegen ob die Ausfallquote mit der Zeit ansteigt (überwiegend
Verschleissausfälle, ![]() ), konstant bleibt (überwiegend
Zufallsausfälle,
), konstant bleibt (überwiegend
Zufallsausfälle, ![]() ) oder abfällt (überwiegend
Frühausfälle,
) oder abfällt (überwiegend
Frühausfälle, ![]() ). Gesondert eingezeichnet ist der Spezialfall
konstanter Ausfallrate, der sich für
). Gesondert eingezeichnet ist der Spezialfall
konstanter Ausfallrate, der sich für
![]() ergibt. Mit
ergibt. Mit
![]() kann man die Lage des Häufungspunktes festlegen.
kann man die Lage des Häufungspunktes festlegen.