|
In Abschnitt 10.4 wurde festgestellt, dass die
Zeitkonstanten etwa gleich sind, die für das Abklingverhalten
verantwortlich sind. Deshalb wird das rechte Verzögerungsglied
![]() in Abbildung 45 auf den gleichen Prozess
zurückgeführt wie das Verzögerungsglied
in Abbildung 45 auf den gleichen Prozess
zurückgeführt wie das Verzögerungsglied ![]() in Abbildung
48. Wird unter Berücksichtigung dieser
Erkenntnis das
in Abbildung
48. Wird unter Berücksichtigung dieser
Erkenntnis das ![]() -System aus Abbildung 45 und
das
-System aus Abbildung 45 und
das ![]() -System aus Abbildung 48 kombiniert, so
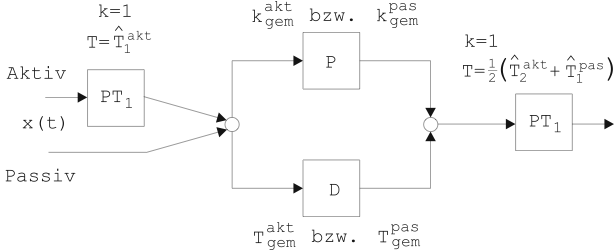
erhält man das gemischte Modell in Abbildung
57, mit dem wir sowohl das aktive als auch das
passive Verhalten modellieren können. Dabei ist zu beachten, dass
nun auch beim aktiven Verhalten differentielle Anteile mitwirken
können. Die zu bestimmenden Parameter dieses Modells lauten im
aktiven Fall
-System aus Abbildung 48 kombiniert, so
erhält man das gemischte Modell in Abbildung
57, mit dem wir sowohl das aktive als auch das
passive Verhalten modellieren können. Dabei ist zu beachten, dass
nun auch beim aktiven Verhalten differentielle Anteile mitwirken
können. Die zu bestimmenden Parameter dieses Modells lauten im
aktiven Fall ![]() als Verstärkungsfaktor für das
proportionale Glied P und
als Verstärkungsfaktor für das
proportionale Glied P und ![]() als Zeitkonstante des
differenziellen Gliedes D. Im passiven Fall lauten die Parameter
analog
als Zeitkonstante des
differenziellen Gliedes D. Im passiven Fall lauten die Parameter
analog ![]() und
und ![]() .
.
Für das passive Verhalten ist es nicht notwendig, eine neue
Parameterbestimmung durchzuführen. Die Parameter ![]() und
und ![]() können direkt aus den schon ermittelten den
Parameterschätzwerten
können direkt aus den schon ermittelten den
Parameterschätzwerten
![]() und
und
![]() in
Tabelle 7 bestimmt werden. Es gilt dabei:
in
Tabelle 7 bestimmt werden. Es gilt dabei:
Führt man nun eine Parameterbestimmung des aktiven Verhaltens für
die Parameter ![]() und
und ![]() wie in Abschnitt
10 für das in Abbildung 57
dargestellte Modell durch, entsteht analog zu Gleichung
33 hier:
wie in Abschnitt
10 für das in Abbildung 57
dargestellte Modell durch, entsteht analog zu Gleichung
33 hier:
Die Parameterschätzwerte ergeben sich damit für die Proben 6-C und
7-C zu:
| Parameter | Mittelwert | Fehlerintervall |
|
|
||
|
|
||
|
|
||
|
|
[ |
|
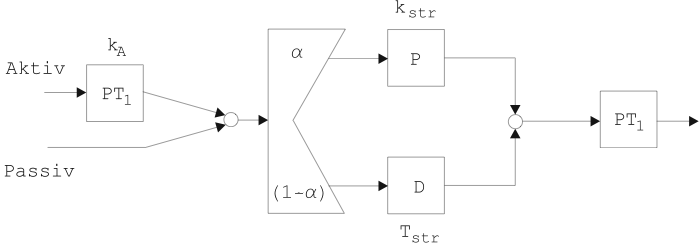
Der Verstärkungsfaktor ![]() im linken
im linken ![]() -Glied, der im
gemischten Modell zuvor auf eins gesetzt wurde, ist hier nicht
bekannt. Ein Aufteilungsglied wird eingeführt, das über die
Gewichtung der differentiellen und proportionalen Anteile
entscheidet. Der Aufteilungsparameter
-Glied, der im
gemischten Modell zuvor auf eins gesetzt wurde, ist hier nicht
bekannt. Ein Aufteilungsglied wird eingeführt, das über die
Gewichtung der differentiellen und proportionalen Anteile
entscheidet. Der Aufteilungsparameter ![]() wird für aktives
(
wird für aktives
(![]() ) und passives (
) und passives (![]() ) Verhalten
unterschiedlich angenommen. Die neu eingeführten
Verstärkungsfaktoren
) Verhalten
unterschiedlich angenommen. Die neu eingeführten
Verstärkungsfaktoren ![]() für das proportionale Glied und
für das proportionale Glied und
![]() für das differenzielle Glied werden jedoch für aktives
und passives Verhalten als gleich angenommen. Die Eigenschaften
der Gewebeanteile, die Kräfte übertragen, seien also sowohl für
passives als auch für aktives Verhalten konstant. Jedoch sollen
die Anteile an der Kraftübertragung im passiven und aktiven Fall
für die Gewebeanteile mit jeweils differenziellen und
proportionalen Verhalten unterschiedlich sein. Damit können wir im
einzelnen schreiben:
für das differenzielle Glied werden jedoch für aktives
und passives Verhalten als gleich angenommen. Die Eigenschaften
der Gewebeanteile, die Kräfte übertragen, seien also sowohl für
passives als auch für aktives Verhalten konstant. Jedoch sollen
die Anteile an der Kraftübertragung im passiven und aktiven Fall
für die Gewebeanteile mit jeweils differenziellen und
proportionalen Verhalten unterschiedlich sein. Damit können wir im
einzelnen schreiben:
|
|
Dies bedeutet, dass bei einer Kontraktion fast nur proportionale
Anteile Kräfte übertragen. Hingegen bei einer passiven Längung des
Gewebes fast nur differentielle Anteile beteiligt sind. Zur
Verdeutlichung: proportionale Anteile sind hier Gewebeanteile, die
wie eine elastische Feder wirken (![]() ), differenzielle
Anteile sind hingegen Gewebeanteile, die wie ein viskoser Dämpfer
wirken (
), differenzielle
Anteile sind hingegen Gewebeanteile, die wie ein viskoser Dämpfer
wirken (![]() ).
).
Denn würden Kräfte bei Kontraktion hauptsächlich über differenzielle Anteile übertragen, so würde der Muskel einen Großteil der geleisteten Arbeit ineffektiverweise in Verformungen stecken und nicht in die erforderliche Kraftschlüssigkeit.
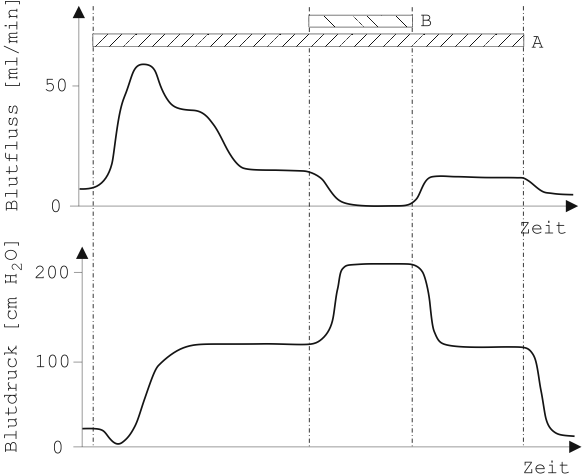
Bei der passiven Längung des Muskels würde hingegen ein zu hoher proportionaler Anteil bedeuten, dass z.B. ein stetiges Füllen des Corpus cavernosum (glatte Muskulatur) mit Blut nur mit einer starken Blutdruckzunahme einhergeht. Erst in Gegenwart von differenziellen Verhalten ist eine Volumenzunahme des Schwellkörpers und damit eine Längung seiner Muskulatur ohne großen Blutdruckanstieg möglich (siehe Abbildung 61). Für das Einstellen einer Erektion nach dem Füllen der Schwellkörper mit Blut sind andere Mechanismen verantwortlich.
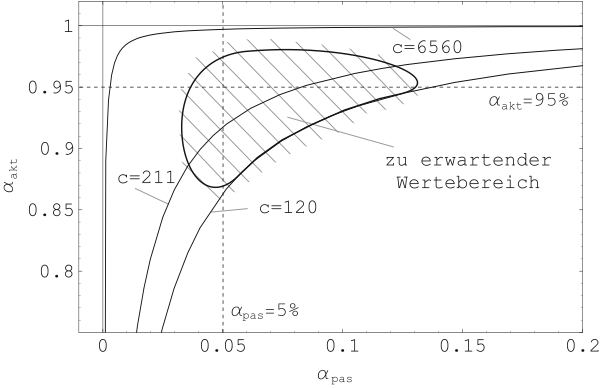
Zusammenfassend kann also geschlossen werden, dass der erschlaffte
Muskel auf langsame Längung sehr nachgiebig reagiert. Bei einer
Aktivierung jedoch steigt die Steifigkeit des Muskels stark an. Im
passiven Fall beträgt ![]() etwa 5% und im aktiven Fall
ist
etwa 5% und im aktiven Fall
ist ![]() ca. 90%. Die Steifigkeit nimmt also etwa auf
das zwanzigfache zu. Bei einer Aktivierung entwickelt die glatte
Muskulatur des Corpus cavernosum also nicht nur eine Kraft
und/oder Längenabnahme, sondern auch die mechanischen
Eigenschaften ändern sich grundlegend.
ca. 90%. Die Steifigkeit nimmt also etwa auf
das zwanzigfache zu. Bei einer Aktivierung entwickelt die glatte
Muskulatur des Corpus cavernosum also nicht nur eine Kraft
und/oder Längenabnahme, sondern auch die mechanischen
Eigenschaften ändern sich grundlegend.
Der große Fehler des Parameters ![]() in Gleichung
44 ist möglicherweise auf eine zu erwartende
Längenabhängigkeit von
in Gleichung
44 ist möglicherweise auf eine zu erwartende
Längenabhängigkeit von ![]() zurückzuführen. Die
Aufteilungverhältnisse für proportionales und differenzielles
Verhalten sind sicherlich längenabhängig. Für eine erste
Abschätzung wurde in dieser Arbeit über alle Längen gemittelt.
zurückzuführen. Die
Aufteilungverhältnisse für proportionales und differenzielles
Verhalten sind sicherlich längenabhängig. Für eine erste
Abschätzung wurde in dieser Arbeit über alle Längen gemittelt.