Oft liegen Daten vor, die durch klassische Verteilungsfunktionen nur mit unvertretbarem Fehler approximiert werden können. Um dennoch die Daten ausreichend gut durch eine analytisch darstellbare Funktion anzunähern, erweitert man die klassischen Verteilungsfunktionen durch ein Verteilungsfunktion-System. Hier wird das Johnson-System betrachtet ([15] Seite 164).
Dieses System entsteht durch Anwendung von drei Transformationen
auf die Normalverteilung
![]() , um diese an verschiedene
Anforderungen anzupassen. Sei
, um diese an verschiedene
Anforderungen anzupassen. Sei
![]() eine
Normalverteilte Zufallsvariable, dann schreiben sich die
Transformationen als
eine
Normalverteilte Zufallsvariable, dann schreiben sich die
Transformationen als
Die Wirkungen dieser Transformationen lassen sich gut im
![]() -Raum darstellen. Für die Parameter
-Raum darstellen. Für die Parameter ![]() und
und ![]() gilt
gilt
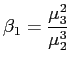 und und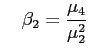 |
(47) |
Dabei sind die ![]() die i. zentralen Momente einer
Zufallsvariablen X, für die gelten
die i. zentralen Momente einer
Zufallsvariablen X, für die gelten
| (48) |
![]() ist hierbei der Erwartungswert (siehe Abschnitt
2.3.1) und
ist hierbei der Erwartungswert (siehe Abschnitt
2.3.1) und ![]() wird als Mittelwert bezeichnet.
wird als Mittelwert bezeichnet.
![]() werden als Schiefe (Skewness) und
werden als Schiefe (Skewness) und ![]() als
Wölbung (Kurtosis) bezeichnet.
als
Wölbung (Kurtosis) bezeichnet.
Die Parameter ![]() und
und ![]() der Johnson Transformationen
sowie die Parameter
der Johnson Transformationen
sowie die Parameter ![]() und
und ![]() der Normalverteilung
lassen sich aus den Größen
der Normalverteilung
lassen sich aus den Größen ![]() ,
, ![]() ,
, ![]() und
und ![]() bestimmen. Für eine genauere Darstellung sei hier auf
[15] Seite 164 verwiesen.
bestimmen. Für eine genauere Darstellung sei hier auf
[15] Seite 164 verwiesen.
In Abbildung E.1 sind die Gebiete, die sich mit den
Transformationen ![]() ,
, ![]() und
und ![]() erreichen lassen im
erreichen lassen im
![]() -Raum dargestellt. Beispielhaft sind auch die
empirischen Verteilungen der Kaufpreise von Geräten aus
verschiedenen Krankenhäusern als Punkte eingezeichnet. Es ist
deutlich zu erkennen, dass die empirischen Kaufpreis-Verteilungen
im
-Raum dargestellt. Beispielhaft sind auch die
empirischen Verteilungen der Kaufpreise von Geräten aus
verschiedenen Krankenhäusern als Punkte eingezeichnet. Es ist
deutlich zu erkennen, dass die empirischen Kaufpreis-Verteilungen
im ![]() -Bereich zu finden sind.
-Bereich zu finden sind.

|